About 4 min
多个字符串的最长公共前缀
// 14. 最长公共前缀
class Solution {
public String longestCommonPrefix(String[] strs) {
char[][] cs = new char[strs.length][];
int minLen = strs[0].length();
for (int i = 0; i < strs.length; i++) {
cs[i] = strs[i].toCharArray();
minLen = Math.min(minLen, cs[i].length);
}
char[] result = new char[minLen];
int resultIdx = 0;
for(int i = 0; i< minLen; i++){
char c = cs[0][i];
int j = 1;
for(; j < cs.length; j++){
if(c != cs[j][i]){
break;
}
}
if(j == cs.length){
result[resultIdx++] = c;
}else{
break;
}
}
return new String(result, 0, resultIdx);
}
}
匹配子串
暴力匹配
手机暴力匹配,效果等同调用 indexOf 函数
class Solution {
public int strStr(String haystack, String needle) {
return haystack.indexOf(needle);
}
}
// 28. 找出字符串中第一个匹配项的下标
class Solution {
public int strStr(String haystack, String needle) {
char[] c1 = haystack.toCharArray();
char[] c2 = needle.toCharArray();
int i = 0, j = 0;
while (i < c1.length && j < c2.length) {
if (c1[i] != c2[j]) {
i = i - j + 1; // 回退j个的下一个。不是直接i++
j = 0; // 清零
} else {
i++;
j++;
}
}
if (j == c2.length) {
return i - c2.length;
} else {
return -1;
}
}
}
KMP
模式串自身的前后缀(不包含自身)匹配。
lps: 下标i处的值表示,i+1个字符的最长公共前缀的个数。
比如,j及其前面有3个已匹配的字符,而3个已匹配的字符的最长公共前缀的个数,对应lps中就是下标2的值。
前进:lps[i] = j + 1,回退:j = lps[j-1]
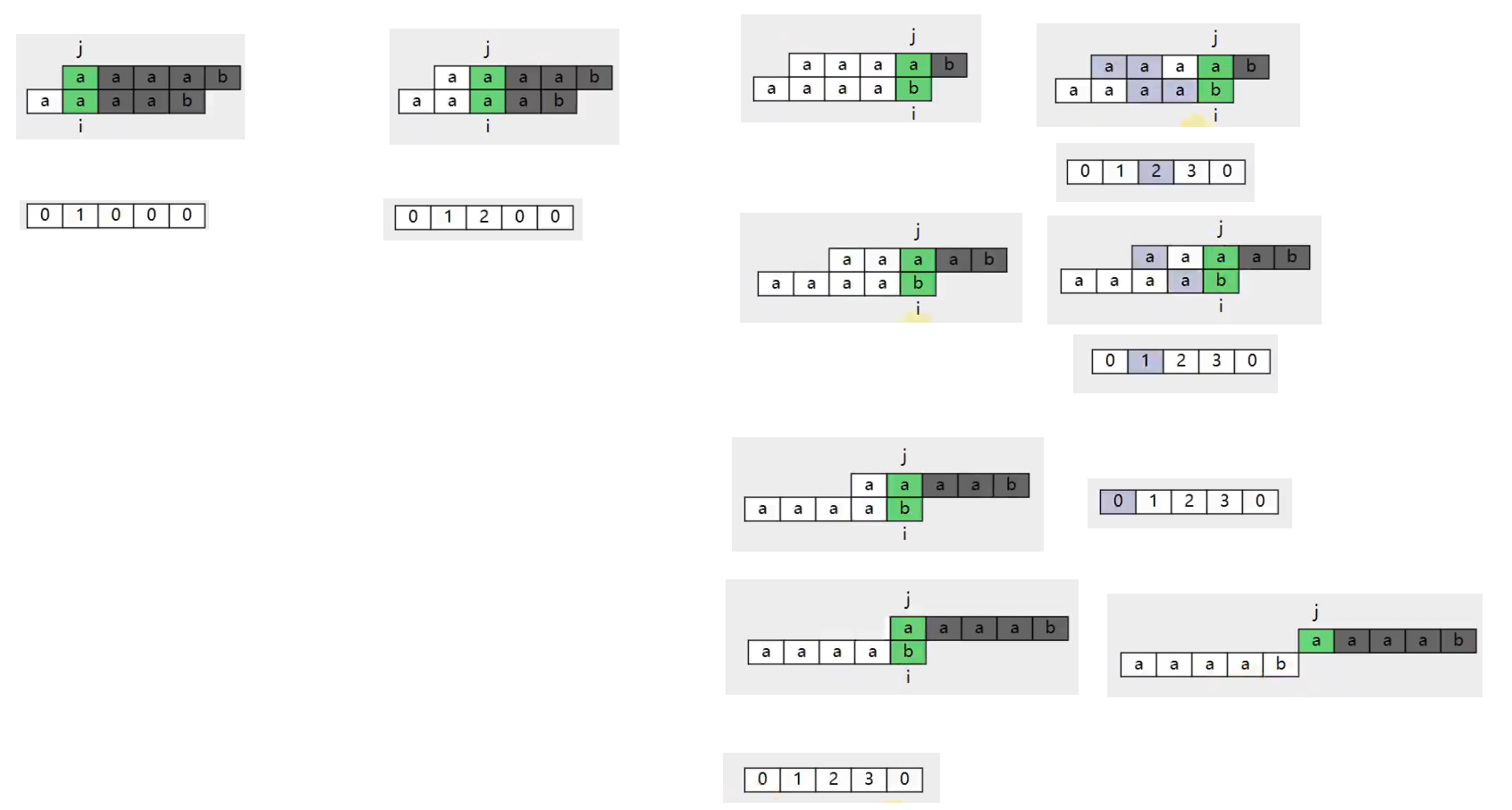
i和j犬牙交错,lps和i同步:
- 第一个字符必然没有前后缀。
- i从1开始,j从0开始。
遍历i,回退是j动i不动
匹配
i和j同步,都从0开始。
// 28. 找出字符串中第一个匹配项的下标
class Solution {
public int strStr(String haystack, String needle) {
char[] origin = haystack.toCharArray();
char[] pattern = needle.toCharArray();
int[] lps = new int[pattern.length];
int i = 1, j = 0;
while (i < pattern.length) {
if (pattern[i] == pattern[j]) {
lps[i] = j + 1;
i++;
j++;
} else {
if (j == 0) { // j已经是0了,不能再退,直接i++
i++;
} else {
j = lps[j - 1];
}
}
}
i = 0;
j = 0;
// while (pattern.length - j <= origin.length - i) { // pattern剩余未匹配的要小于等于origin剩余未匹配的。没必要,ms都看不出来
while (i < origin.length) {
if (origin[i] == pattern[j]) {
i++;
j++;
} else {
if (j == 0) {
i++;
} else {
j = lps[j - 1];
}
}
// 匹配完所有模式串字符
if (j == pattern.length) {
return i - j;
}
}
return -1;
}
}
重复的子字符串
观察特性:
我们可以把字符串 s 写成 $s's'\cdots s'$ 的形式,$s'$就是重复子串。
如果我们移除字符串 s 的前n'个字符(一个完整的 $s'$),再将这些字符保持顺序添加到剩余字符串的末尾,那么得到的字符串仍然是 s。
那么如果将两个 s 连在一起(相当于s的头尾拼接了),并移除第一个和最后一个字符(不让它匹配首个和最后的重复字符串),那么得到的字符串一定包含 s,即s 是它的一个子串。
最简单:
// 459. 重复的子字符串
class Solution {
public boolean repeatedSubstringPattern(String s) {
String str = s + s;
// return str.indexOf(s, 1) != s.length();
return str.substring(1, str.length() - 1).contains(s);
}
}
用KMP来写 contains()
// 459. 重复的子字符串
class Solution {
public boolean repeatedSubstringPattern(String s) {
return kmp(s + s, s);
}
public boolean kmp(String s1, String s2) {
char[] origin = s1.toCharArray();
char[] pattern = s2.toCharArray();
int[] lps = new int[pattern.length];
int i = 1, j = 0;
while(i<pattern.length){
if(pattern[i] == pattern[j]){
lps[i] = j + 1;
i++;
j++;
} else{
if(j == 0){
i++;
}else{
j = lps[j - 1];
}
}
}
i = 1; // 去掉头部
j = 0;
while(i < origin.length - 1){ // 去掉尾部
if(origin[i] == pattern[j]){
i++;
j++;
} else{
if(j == 0){
i++;
}else{
j = lps[j - 1];
}
}
if(j == pattern.length){
return true;
}
}
return false;
}
}
最长回文子串
检测方式:以下标i为圆心,向两边同步扩展。
两种回文:单个下标i开始,两个下标i和i+1开始。
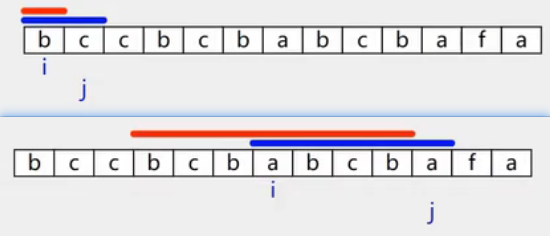
// 5.最长回文子串
class Solution {
int left;
int right;
public String longestPalindrome(String s) {
char[] cs = s.toCharArray();
for (int i = 0; i < s.length(); i++) {
extend(cs, i, i);
if (i <= s.length() - 1)
extend(cs, i, i + 1);
}
return new String(cs, left, right - left + 1);
}
public void extend(char[] cs, int i, int j) {
while (i >= 0 && j < cs.length && cs[i] == cs[j]) {
i--;
j++;
}
// while超了,还原
i++;
j--;
if (j - i > right - left) {
left = i;
right = j;
}
}
}
最小覆盖子串
字典统计:确定覆盖子串
一旦覆盖:缩小i
// 76.最小覆盖子串
class Solution {
boolean flag;
int left;
int right;
public String minWindow(String s, String t) {
char[] cs = s.toCharArray();
char[] ct = t.toCharArray();
// 字符字典,统计不同字符的个数
int[] scount = new int[128];
int[] tcount = new int[128];
// 有几种字符是存在的
int condition = 0;
for (char c : ct) {
tcount[c]++;
}
for (int tc : tcount) {
if (tc > 0)
condition++;
}
int i = 0;
int tempCondition = 0;
// 遍历 s 字符串
for(int j = 0; j < cs.length; j++){
char cj = cs[j];
scount[cj]++;
if (scount[cj] == tcount[cj]) {
tempCondition++;
}
// 缩小i:条件满足且i不超过j
while (condition == tempCondition && i <= j) {
// 判断当前 [i...j] 部分
// 第一次
if (!flag) {
left = i;
right = j;
flag = true;
} else if (j - i < right - left) {
left = i;
right = j;
}
// 更新i
char ci = cs[i];
scount[ci]--;
if (scount[ci] < tcount[ci]) {
tempCondition--;
}
i++;
}
}
return flag ? new String(cs, left, right - left + 1) : "";
}
}