About 2 min
一维
前缀和
对于数组 nums,定义它的前缀和
- $nums[0]=0$
- $nums[i+1] = \sum\limits_{j=0}^{i}\textit{nums}[j]$。
根据这个定义,有 sums[i+1]=sums[i]+nums[i]
例如 nums=[1,2,1,2],对应的前缀和数组为 sums=[0,1,3,4,6]。
sums[i]表示[0...i-1]的子数组的和,sums[0]=0 表示一个空数组的元素和。
前缀和之差
把子数组的元素和转换成两个前缀和的差,即
[left...right] = sums[right + 1] - sums[left]
$$\displaystyle \sum_{j=left}^{right}\textit{nums}[j] = sums[right+1] - sums[left] = \sum\limits_{j=0}^{right} \textit{nums}[j] - \sum\limits_{j=0}^{left-1}\textit{nums}[j] $$
问:为什么要定义 sums[0]=0,这样做有什么好处?
答:如果要计算的子数组是[0...j],那么就是sums[j+1]-sums[0]。如果不定义 sums[0]=0,就必须特判 left=0 的情况了。
// 303. 区域和检索 - 数组不可变
class NumArray {
int[] sums;
public NumArray(int[] nums) {
sums = new int[nums.length + 1];
sums[0] = 0;
for (int i = 0; i < nums.length; i++) {
sums[i + 1] = sums[i] + nums[i];
}
}
public int sumRange(int left, int right) {
return sums[right + 1] - sums[left];
}
}
二维
// 304. 二维区域和检索 - 矩阵不可变
class NumMatrix {
int[][] sums;
public NumMatrix(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
sums = new int[m + 1][n + 1];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
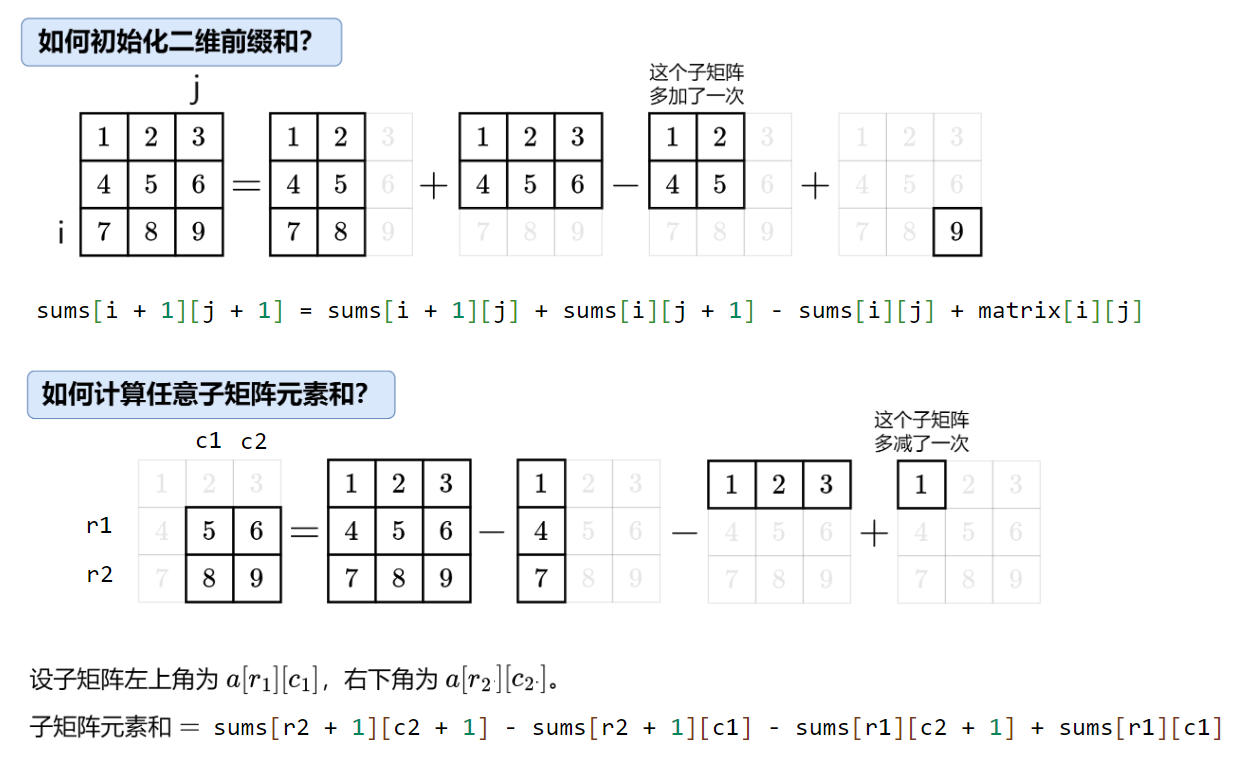
sums[i + 1][j + 1] = sums[i + 1][j] + sums[i][j + 1] - sums[i][j] + matrix[i][j];
}
}
}
// 返回左上角在 (r1,c1) 右下角在 (r2,c2) 的子矩阵元素和
public int sumRegion(int r1, int c1, int r2, int c2) {
return sums[r2 + 1][c2 + 1] - sums[r2 + 1][c1] - sums[r1][c2 + 1] + sums[r1][c1];
}
}