About 5 min
总结
- 不剪枝;全排列 (vis);组合和组合总和 (sort后放入更大);
- 组合 (剩余个数);组合总和 (target)
不剪枝
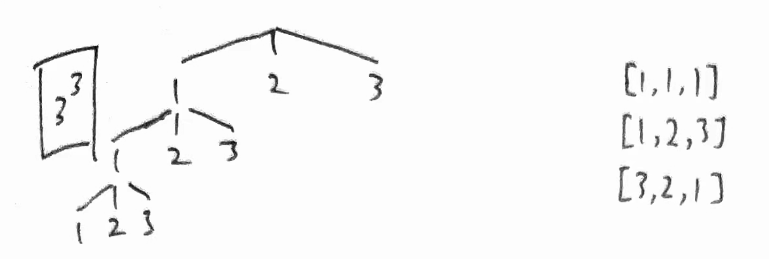
全排列
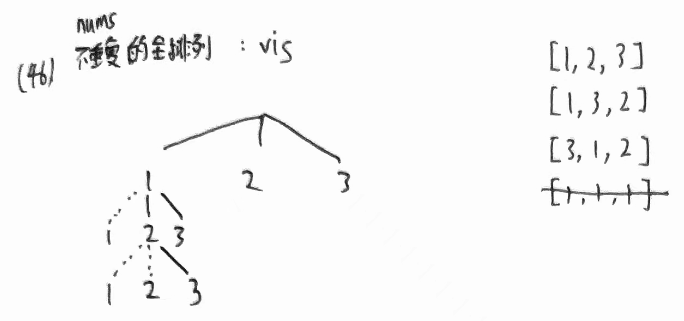
组合: sort后放入更大,是包含了vis 1-2-3 和 排列的重复解 3-2-1
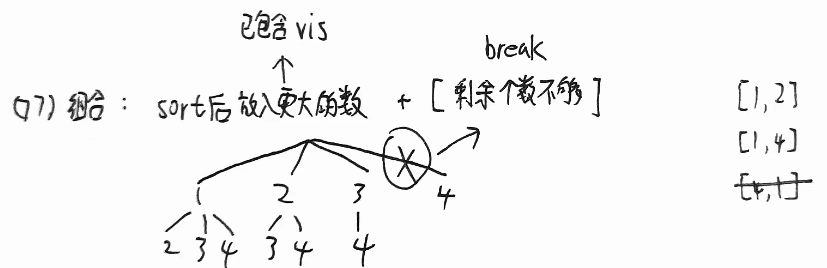
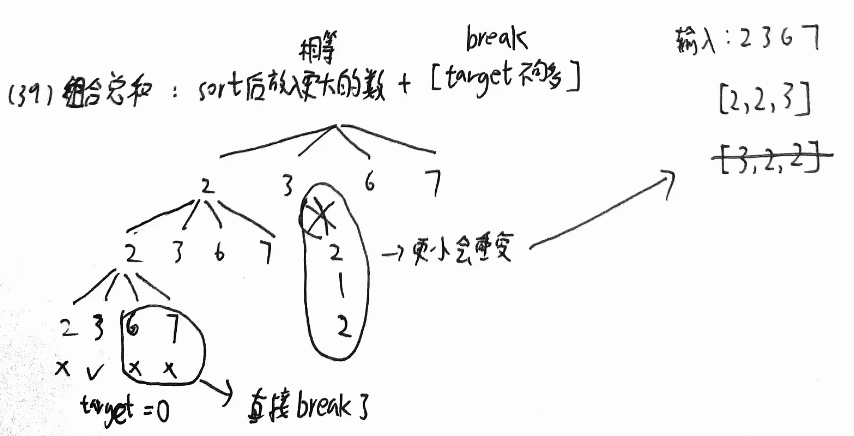
组合总和
不剪枝
// 回溯
class Solution {
// 保存每条从根到叶子的链路
LinkedList<Integer> stack = new LinkedList<>();
int[] nums;
// 所有的链路
List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
this.nums = nums;
dfs();
return result;
}
public void dfs() {
if (stack.size() == nums.length) {
// 注意添加子列表时,直接引用对象会被修改,要clone新对象。
result.add(new ArrayList<>(stack));
return;
}
for (int i = 0; i < nums.length; i++) {
// 正向操作:放入
stack.push(nums[i]);
dfs(); // 放入,拿出 = 回溯
// 反向操作:拿出
stack.pop();
}
}
}
/ [1, 2, 3]
// [[1,1,1],[2,1,1],[3,1,1],[1,2,1],[2,2,1],[3,2,1],[1,3,1],[2,3,1],[3,3,1],[1,1,2],[2,1,2],[3,1,2],[1,2,2],[2,2,2],[3,2,2],[1,3,2],[2,3,2],[3,3,2],[1,1,3],[2,1,3],[3,1,3],[1,2,3],[2,2,3],[3,2,3],[1,3,3],[2,3,3],[3,3,3]]
46. 全排列
剪枝
- 已遍历vis
// leetcode 46
// 回溯 + 剪枝
class Solution {
// 保存每条从根到叶子的链路
LinkedList<Integer> stack = new LinkedList<>();
int[] nums;
// 所有的链路
List<List<Integer>> result = new ArrayList<>();
// 剪枝:已遍历的节点
boolean[] vis;
public List<List<Integer>> permute(int[] nums) {
vis = new boolean[nums.length];
this.nums = nums;
dfs();
return result;
}
public void dfs() {
if (stack.size() == nums.length) {
// 注意添加子列表时,直接引用对象会被修改,要clone新对象。
result.add(new ArrayList<>(stack));
return;
}
for (int i = 0; i < nums.length; i++) {
if(vis[i]){
continue;
}
// 正向操作:放入、标记已遍历
stack.push(nums[i]);
vis[i] = true;
dfs();
// 反向操作:拿出、取消标记
vis[i] = false;
stack.pop();
}
}
}
// [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
47. 全排列 II
剪枝
- 已遍历vis
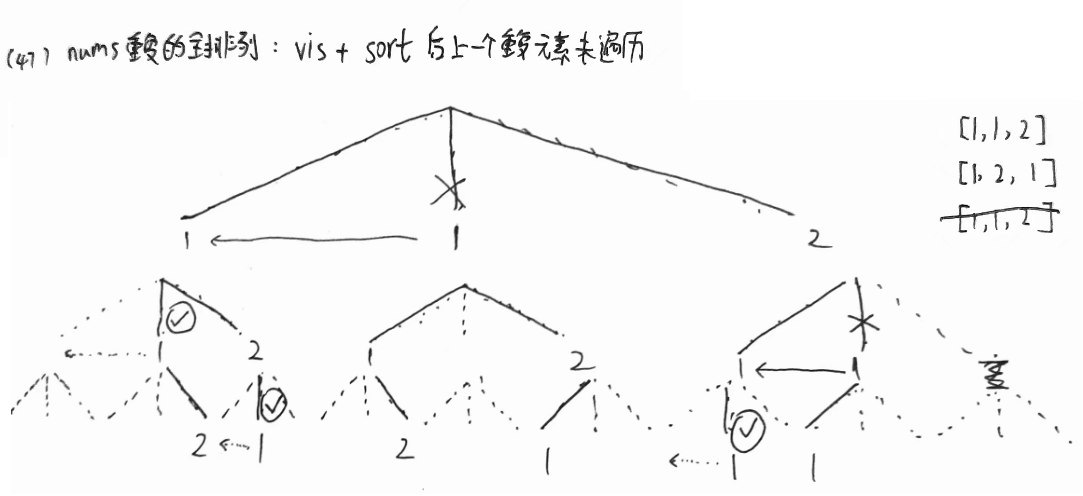
- nums逆序重复:排序数组后,剪去逆序的枝叶(第二个1-第一个1-2),只保留顺序的枝叶(第一个1-第二个1-2):如果前一个重复元素已经访问过了,那说明是顺序下的新解;没访问过,说明是逆序的老解。
class Solution {
// 保存每条从根到叶子的链路
LinkedList<Integer> stack = new LinkedList<>();
int[] nums;
// 所有的链路
List<List<Integer>> result = new ArrayList<>();
// 剪枝:已遍历的节点
boolean[] vis;
public List<List<Integer>> permuteUnique(int[] nums) {
vis = new boolean[nums.length];
this.nums = nums;
Arrays.sort(this.nums);
dfs();
return result;
}
public void dfs() {
if (stack.size() == nums.length) {
// 注意添加子列表时,直接引用对象会被修改,要clone新对象。
result.add(new ArrayList<>(stack));
return;
}
for (int i = 0; i < nums.length; i++) {
// 已遍历vis
if (vis[i])
continue;
// 剪去逆序的枝叶
if (i > 0 && nums[i] == nums[i - 1] && !vis[i - 1])
continue;
// 正向操作:放入、标记已遍历
stack.push(nums[i]);
vis[i] = true;
dfs();
// 反向操作:拿出、取消标记
vis[i] = false;
stack.pop();
}
}
}
77. 组合
剪枝
- 放入更大的数:已包含了已遍历vis
- 剩余个数不够时
class Solution {
int k;
int n;
// 保存每条从根到叶子的链路
LinkedList<Integer> stack = new LinkedList<>();
// 所有的链路
List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> combine(int n, int k) {
this.k = k;
this.n = n;
dfs();
return result;
}
public void dfs() {
if (stack.size() == k) {
// 注意添加子列表时,直接引用对象会被修改,要clone新对象。
result.add(new ArrayList<>(stack));
return;
}
int i = 1;
if (!stack.isEmpty()) {
i = stack.peek() + 1; // 放入更大的数:包含了已遍历vis的情况
}
for (; i <= n; i++) {
// 剩余个数不够时,剪枝
if(k - stack.size() > n - i + 1){
break;
}
stack.push(i);
dfs();
stack.pop();
}
}
}
39. 组合总和
class Solution {
// 保存每条从根到叶子的链路
LinkedList<Integer> stack = new LinkedList<>();
// 所有的链路
List<List<Integer>> result = new ArrayList<>();
int[] nums;
int target;
public List<List<Integer>> combinationSum(int[] candidates, int target) {
this.nums = candidates;
this.target = target;
Arrays.sort(this.nums);
dfs();
return result;
}
public void dfs() {
if (target == 0) {
// 注意添加子列表时,直接引用对象会被修改,要clone新对象。
result.add(new ArrayList<>(stack));
return;
}
for (int i = 0; i < nums.length; i++) {
// 剪枝大小逆序而重复的:2-2-3,3-2-2,2-3-2中的3-2-2,2-3-2
if (!stack.isEmpty() && nums[i] < stack.peek())
continue;
// 剪枝剩余target超了的
if (target - nums[i] < 0)
break;
stack.push(nums[i]);
target -= nums[i];
dfs();
target += nums[i];
stack.pop();
}
}
}
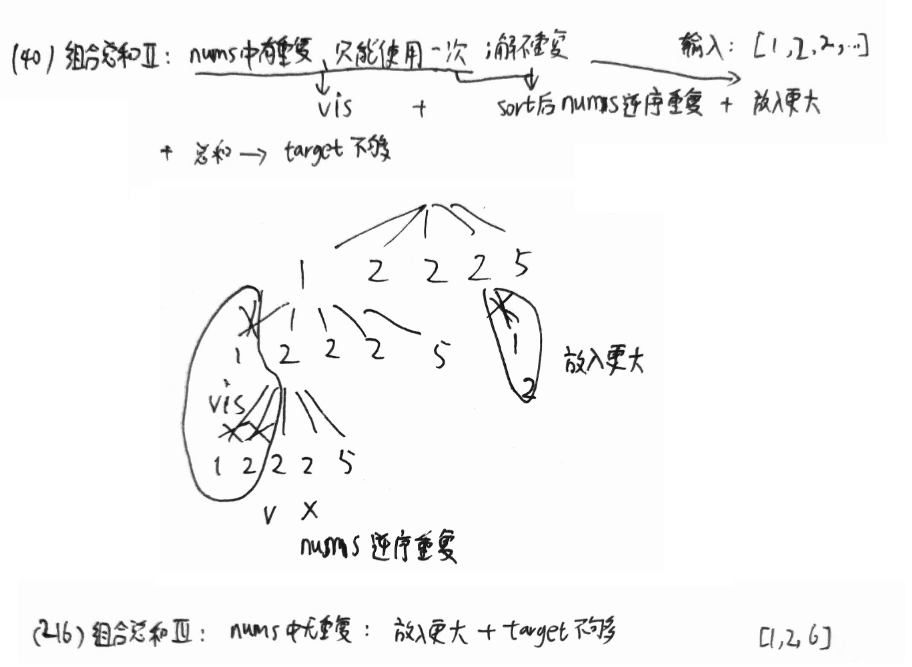
40. 组合总和 II
class Solution {
// 保存每条从根到叶子的链路
LinkedList<Integer> stack = new LinkedList<>();
// 所有的链路
List<List<Integer>> result = new ArrayList<>();
int[] nums;
boolean[] vis;
int target;
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
this.nums = candidates;
vis = new boolean[nums.length];
this.target = target;
Arrays.sort(this.nums);
dfs();
return result;
}
public void dfs() {
if (target == 0) {
// 注意添加子列表时,直接引用对象会被修改,要clone新对象。
result.add(new ArrayList<>(stack));
return;
}
for (int i = 0; i < nums.length; i++) {
// 已遍历
if (vis[i])
continue;
// nums逆序重复
if (i > 0 && nums[i] == nums[i - 1] && !vis[i - 1])
continue;
// 剪枝大小逆序而重复的:2-2-3,3-2-2,2-3-2中的3-2-2,2-3-2
if (!stack.isEmpty() && nums[i] < stack.peek())
continue;
// 剪枝剩余target超了的
if (target - nums[i] < 0)
break;
stack.push(nums[i]);
target -= nums[i];
vis[i] = true;
dfs();
vis[i] = false;
target += nums[i];
stack.pop();
}
}
}
216. 组合总和 III
- 放入更大的数:包含了已遍历vis
- 剪枝剩余target超了的
class Solution {
// 保存每条从根到叶子的链路
LinkedList<Integer> stack = new LinkedList<>();
// 所有的链路
List<List<Integer>> result = new ArrayList<>();
int k;
int n = 9;
int target;
public List<List<Integer>> combinationSum3(int k, int n) {
this.target = n;
this.k = k;
dfs();
return result;
}
public void dfs() {
// 个数且target满足
if (stack.size() == k && target == 0) {
// 注意添加子列表时,直接引用对象会被修改,要clone新对象。
result.add(new ArrayList<>(stack));
return;
}
int i = 1;
if (!stack.isEmpty()) {
i = stack.peek() + 1; // 放入更大的数:包含了已遍历vis的情况
}
for (; i <= n; i++) {
// 剪枝剩余target超了的
if (target - i < 0)
break;
stack.push(i);
target -= i;
dfs();
target += i;
stack.pop();
}
}
}