• 1.两数之和
• 167.两数之和 II
• n数和
  • 15.三数之和
  • 18.四数之和

---

1.两数之和

用hash做。

我们要获取，num[i]和它的对应元素target-nums[i] 的下标。

那就遍历每个元素，hash存元素 key 和它的下标 value。

如果发现 target-nums[i]存在，那么就不用存当前元素了，直接return 输出。

class Solution {
    public int[] twoSum(int[] nums, int target) {
        HashMap<Integer, Integer> map = new HashMap<>();
        for(int i = 0; i<nums.length; i++){
            int another = target - nums[i];
            Integer v = map.get(another);
            if(v == null){
                map.put(nums[i], i);
            }
            else{
                return new int[]{v , i};
            }
        }
        return null;
    }
}

167.两数之和 II

有序数组、只需返回一个解

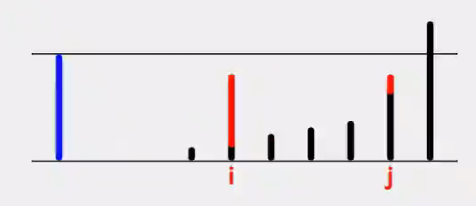
头尾指针。

sum > target ， j--

sum < target, i++

sum == target，返回ij

i == j ， return null

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        for (int i = 0, j = numbers.length - 1; i != j;) {
            int sum = numbers[i] + numbers[j];
            if (sum == target) {
                return new int[] { i + 1, j + 1 };
            } else if (sum > target) {
                j--;
            } else {
                i++;
            }
        }
        return null;
    }
}

n数和

15.三数之和

只用 dfs 超时：因为不能一开始根据k和j已就排除整个子树。

// 40的解法套过来
class Solution {
    // 保存每条从根到叶子的链路
    LinkedList<Integer> stack = new LinkedList<>();
    // 所有的链路
    List<List<Integer>> result = new ArrayList<>();
    int[] nums;
    boolean[] vis;
    int target;

    public List<List<Integer>> threeSum(int[] nums) {
        this.nums = nums;
        this.target = 0;
        vis = new boolean[nums.length];
        Arrays.sort(this.nums);
        dfs();
        return result;
    }

    public void dfs() {
        if(stack.size() == 3){
            if (target == 0) {
                // 注意添加子列表时，直接引用对象会被修改，要clone新对象。
                result.add(new ArrayList<>(stack));
            }
            return;
        }

        for (int i = 0; i < nums.length; i++) {
            // 已遍历
            if (vis[i])
                continue;
            // nums逆序重复
            if (i > 0 && nums[i] == nums[i - 1] && !vis[i - 1])
                continue;
            // 剪枝大小逆序而重复的：2-2-3，3-2-2，2-3-2中的3-2-2，2-3-2
            if (!stack.isEmpty() && nums[i] < stack.peek())
                continue;
            // 剪枝剩余target超了的
            if (target - nums[i] < 0)
                break;
            
            stack.push(nums[i]);
            target -= nums[i];
            vis[i] = true;
            dfs();
            vis[i] = false;
            target += nums[i];
            stack.pop();
        }
    }
}

通用解法：dfs + 两数和，36ms

n表示n数和，dfs里的i表示固定的数后面的元素。

class Solution {
    int[] nums;
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> stack = new LinkedList<>();

    public List<List<Integer>> threeSum(int[] nums) {
        this.nums = nums;
        Arrays.sort(this.nums);
        dfs(3, 0, nums.length - 1, 0);
        return result;
    }

    public void dfs(int n, int i, int j, int target) {
        if (n == 2) {
            twoSum(i, j, target);
            return;
        }

        // n - 2：2表示余2个数进行两数组合，n-2表示n位数去掉2个数来进行遍历的范围
        for (int k = i; k < j - (n - 2); k++) {
            // 重复解
            if (k > i && nums[k] == nums[k - 1]) {
                continue;
            }
            // 都是大于target，就无解
            if (nums[k] > target) {
                break;
            }
            stack.push(nums[k]);
            dfs(n - 1, k + 1, j, target - nums[k]);
            stack.pop();
        }
    }

    public void twoSum(int i, int j, int sumTarget) {
        while (i < j) {
            int sum = nums[i] + nums[j];
            if (sum < sumTarget) {
                i++;
            } else if (sum == sumTarget) {
                List<Integer> t = new ArrayList<>(stack);
                t.add(nums[i]);
                t.add(nums[j]);
                result.add(t);
                i++;
                j--;
                // 重复解
                while (i < j && nums[i] == nums[i - 1]) {
                    i++;
                }
                while (i < j && nums[j] == nums[j + 1]) {       // j+1
                    j--;
                }
            } else {
                j--;
            }

        }
    }
}

道理一样，化递归为循环的写法：27ms

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        Arrays.sort(nums);
        List<List<Integer>> res = new ArrayList<>();
        int target = 0;
        for (int i = 0; i < nums.length - 2; i++) {
            // 重复解
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }
            // 都是大于target，就无解
            if (nums[i] > target) {
                break;
            }
            int target_sum = target - nums[i];
            // 两外两个数，j是正着走，k是倒着走
            int j = i + 1;
            int k = nums.length - 1;
            while(j < k){
                int sum = nums[j] + nums[k];
                if (sum < target_sum) {
                    j++;
                }
                else if (sum == target_sum) {
                    List<Integer> tuple = new ArrayList<>();
                    tuple.add(nums[i]);
                    tuple.add(nums[j]);
                    tuple.add(nums[k]);
                    res.add(tuple);
                    j++;
                    k--;
                    // 重复解
                    while (j < k && nums[j] == nums[j - 1]) {
                        j++;
                    }
                    while (j < k && nums[k] == nums[k + 1]) {       // k+1
                        k--;
                    }
                }else{
                    k--;    
                }
            }
        }
        return res;
    }
}

18.四数之和

把上面的三数通用dfs+两数组合，搬运下来。

class Solution {
    int[] nums;
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> stack = new LinkedList<>();

    public List<List<Integer>> fourSum(int[] nums, int target) {
        this.nums = nums;
        Arrays.sort(this.nums);
        dfs(4, 0, nums.length - 1, target);
        return result;
    }

    public void dfs(int n, int i, int j, long target) {
        if (n == 2) {
            twoSum(i, j, target);
            return;
        }

        // n - 2：2表示余2个数进行两数组合，n-2表示n位数去掉2个数来进行遍历的范围
        for (int k = i; k < j - (n - 2); k++) {
            // 重复解
            if (k > i && nums[k] == nums[k - 1]) {
                continue;
            }
            stack.push(nums[k]);
            dfs(n - 1, k + 1, j, target - nums[k]);
            stack.pop();
        }
    }

    public void twoSum(int i, int j, long sumTarget) {
        while (i < j) {
            long sum = nums[i] + nums[j];
            if (sum < sumTarget) {
                i++;
            } else if (sum == sumTarget) {
                List<Integer> t = new ArrayList<>(stack);
                t.add(nums[i]);
                t.add(nums[j]);
                result.add(t);
                i++;
                j--;
                // 重复解
                while (i < j && nums[i] == nums[i - 1]) {
                    i++;
                }
                while (i < j && nums[j] == nums[j + 1]) {       // j+1
                    j--;
                }
            } else {
                j--;
            }

        }
    }
}